Ukuran Distribusi Data: Panduan Lengkap

Skewness dan Kurtosis adalah ukuran statistik yang digunakan untuk menggambarkan bentuk dan karakteristik suatu distribusi dalam statistik. Skewness adalah ukuran simetri (atau lebih spesifik, kurangnya simetri dalam kumpulan data), yang dapat bernilai positif atau negatif. Sebaliknya, Kurtosis mengukur ekor distribusi (yaitu, mengukur ekstremitas outlier dalam distribusi). Artikel ini akan membahas secara singkat Skewness dan Kurtosis serta persamaan dan perbedaannya.

Kita selalu mencari skewness dan kurtosis saat menganalisis data atau melakukan Exploratory Data Analysis. Kedua ukuran ini memberikan informasi tentang bentuk distribusi, tetapi keduanya menangkap aspek data yang berbeda. Skewness mengukur derajat asimetri dalam distribusi, sedangkan kurtosis mengukur derajat keruncingan atau kepuncakan.

Artikel ini akan menjelaskan apa itu skewness dan kurtosis serta perbedaan di antara keduanya.

Perbedaan antara Kemiringan dan Kurtosis

Parameter	Kemiringan	Kurtosis
Definisi	Mengukur derajat asimetri dari distribusi.	Mengukur derajat ketajaman dari distribusi.
Perhitungan	Merupakan momen ketiga dari distribusi.	Merupakan momen keempat dari distribusi.
Rentang Nilai	Nilai berkisar dari -tak terhingga hingga +tak terhingga.	Nilai berkisar dari -tak terhingga hingga +tak terhingga.
Interpretasi Nilai	Kemiringan Negatif: Menunjukkan ekor panjang di sisi kiri. Kemiringan Nol: Menunjukkan simetri sempurna. Kemiringan Positif: Menunjukkan ekor panjang di sisi kanan.	Platykurtik: Menunjukkan puncak yang lebih datar daripada distribusi normal. Juga disebut sebagai Kurtosis Negatif. Kurtosis Nol: Menunjukkan normalitas sempurna. Leptokurtik: Menunjukkan puncak yang lebih tajam daripada distribusi normal. Juga disebut sebagai Kurtosis Positif.
Dampak pada Distribusi	Kemiringan dapat mempengaruhi pusat distribusi. Distribusi asimetris memiliki dampak yang lebih besar pada rata-rata daripada median.	Kurtosis dapat mempengaruhi ekor distribusi. Distribusi dengan kurtosis tinggi memiliki nilai ekstrem yang lebih besar dan dapat menyebabkan kesalahan standar yang lebih besar.
Contoh Distribusi	Pendapatan, kekayaan, dan pengembalian saham sering kali memiliki kemiringan positif. Distribusi seperti pensiun dan usia dapat dilihat sebagai kemiringan negatif.	Nilai ujian, skor IQ, dan waktu reaksi sering kali memiliki leptokurtik. Distribusi platykurtik termasuk pendapatan, tinggi badan, dan berat badan.

Apa itu Skewness?

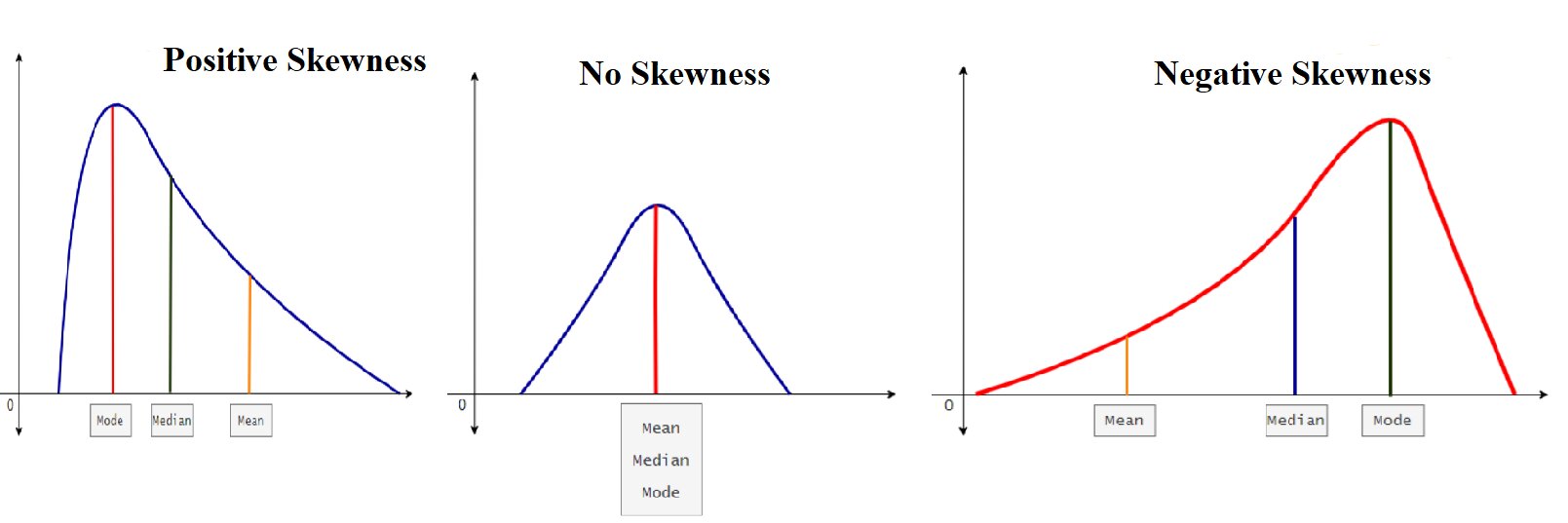
Skewness menentukan bentuk distribusi. Biasanya, kita mendapatkan banyak distribusi asimetris, dan distribusi-distribusi ini memiliki penyebaran data yang tidak merata. Ada dua jenis skewness - positif atau condong ke kanan dan negatif atau condong ke kiri.

Skewness positif terjadi ketika distribusi berlangsung sedemikian rupa sehingga kita mendapatkan ekor panjang di sisi kanan grafik. Ini disebut grafik condong ke kanan. Dalam distribusi ini, nilai rata-rata lebih besar dari nilai median, yang lebih besar dari modus. Artinya, kita mendapatkan rata-rata > median > modus. Skewness negatif terjadi ketika distribusi berlangsung sedemikian rupa sehingga kita mendapatkan ekor panjang di sisi kiri grafik. Ini disebut grafik condong ke kiri.

Apa itu Kurtosis?

Kurtosis adalah ukuran statistik yang menggambarkan derajat keruncingan atau kerataan suatu distribusi. Kurtosis mengukur bentuk distribusi, terutama ketinggian dan ketajaman puncak sentral, relatif terhadap distribusi normal. Kurtosis merupakan momen keempat dari statistik.

Istilah "Kurtosis" berasal dari kata Yunani "Kurtos" yang berarti melengkung. Kurtosis berguna untuk mengidentifikasi kemungkinan adanya outlier dalam sebuah dataset, karena distribusi dengan kurtosis tinggi memiliki nilai-nilai ekstrem yang lebih banyak daripada distribusi normal.

Jenis-Jenis Kurtosis

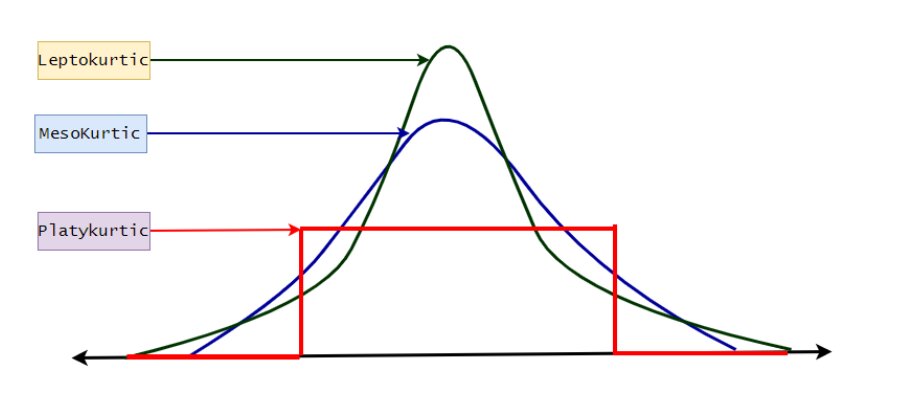
• Mesokurtik: Jenis distribusi ini memiliki simetri. Artinya, kedua ujung ekstrem grafik serupa. Ini sama dengan distribusi normal.

• Leptokurtik: Distribusi ini memiliki kurtosis yang lebih besar dari mesokurtik, dengan ekor yang lebih panjang. Ini menunjukkan bahwa persentase data yang lebih signifikan hadir di dekat ekor, yang menyebabkan ekor menjadi lebih panjang.

• Platikurtik: Distribusi ini memiliki kurtosis yang lebih rendah dari mesokurtik. Artinya, ekornya lebih pendek. Ini berarti ada lebih sedikit data pada bagian ekor, yang membuat ekor menjadi lebih rata.

Perbedaan Utama Antara Skewness dan Kurtosis

• Skewness mengukur derajat asimetri distribusi, sementara Kurtosis mengukur derajat ketajaman dan kelandaian distribusi.

• Skewness adalah ukuran momen ketiga, sedangkan kurtosis adalah ukuran momen keempat.

• Nilai Skewness dan Kurtosis berkisar dari -infinity hingga +infinity.

• Skewness nol dan kurtosis nol mewakili simetri sempurna dan normalitas sempurna.

• Skewness dapat mempengaruhi pusat distribusi, sementara kurtosis dapat mempengaruhi ekor distribusi.

• Keduanya, Skewness dan Kurtosis, menggambarkan bentuk distribusi.