Ide-Ide Utama di Balik Distribusi Normal

1. Apa Itu Distribusi Normal?
Distribusi normal, juga dikenal sebagai distribusi Gaussian, adalah distribusi probabilitas yang simetris terhadap rata-rata, menunjukkan bahwa data yang mendekati rata-rata lebih sering terjadi dibandingkan data yang jauh dari rata-rata. Distribusi normal terlihat seperti "kurva lonceng" saat digrafikkan.
2. Properti Distribusi Normal
Distribusi normal adalah jenis distribusi yang paling umum diasumsikan dalam analisis pasar saham teknis. Distribusi normal standar memiliki dua parameter: rata-rata (mean) dan simpangan baku (standard deviation). Dalam distribusi normal, mean (rata-rata), median (titik tengah), dan modus (observasi paling sering) adalah sama. Nilai-nilai ini mewakili puncak atau titik tertinggi. Distribusi kemudian jatuh secara simetris di sekitar mean, dengan lebar yang ditentukan oleh simpangan baku.
Model distribusi normal adalah kunci untuk Teorema Batas Tengah (CLT) yang menyatakan bahwa rata-rata yang dihitung dari variabel acak yang independen dan terdistribusi identik memiliki distribusi yang kira-kira normal, terlepas dari jenis distribusi dari mana variabel-variabel tersebut diambil.
Distribusi normal adalah salah satu jenis distribusi simetris. Distribusi simetris terjadi ketika garis pembagi menghasilkan dua gambar cermin. Tidak semua distribusi simetris adalah normal karena beberapa data dapat muncul sebagai dua puncak atau serangkaian bukit selain kurva lonceng yang menunjukkan distribusi normal.
3. Pengamatan
Aturan Empiris
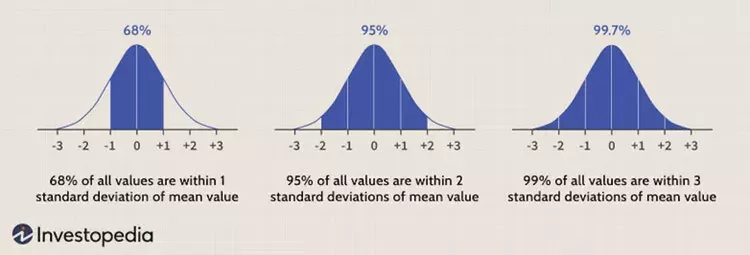
Untuk semua distribusi normal, 68,2% pengamatan akan muncul dalam plus atau minus satu simpangan baku dari mean; 95,4% akan jatuh dalam +/- dua simpangan baku; dan 99,7% dalam +/- tiga simpangan baku.
Fakta ini kadang-kadang disebut sebagai "aturan empiris," sebuah heuristik yang menggambarkan di mana sebagian besar data dalam distribusi normal akan muncul. Data yang jatuh di luar tiga simpangan baku ("3-sigma") akan menunjukkan kejadian langka.
Skewness
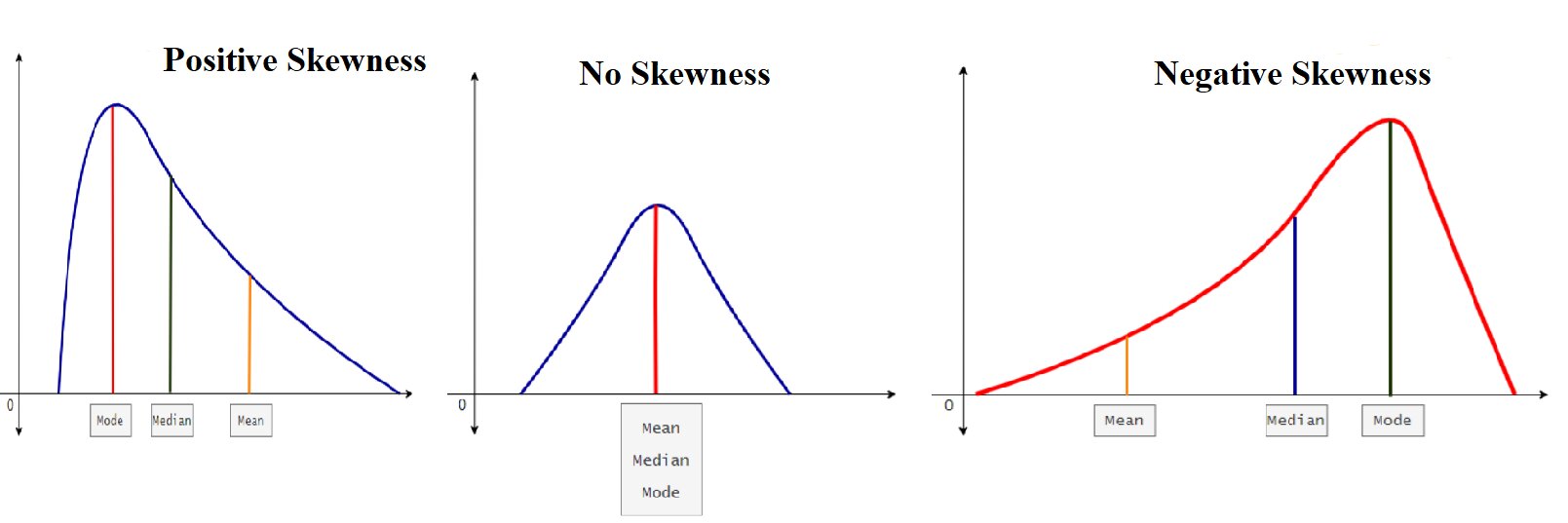
Skewness mengukur derajat simetri dari distribusi. Distribusi normal adalah simetris dan memiliki skewness nol. Jika distribusi dari suatu set data memiliki skewness kurang dari nol, atau skewness negatif (skewness kiri), maka ekor kiri distribusi lebih panjang daripada ekor kanan; skewness positif (skewness kanan) berarti ekor kanan distribusi lebih panjang daripada ekor kiri.
Kurtosis
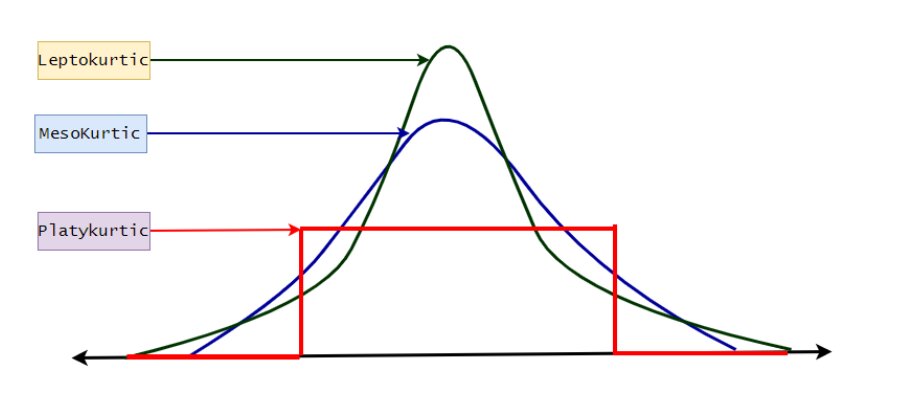
Kurtosis mengukur ketebalan ujung ekor distribusi dibandingkan dengan ekor distribusi. Distribusi normal memiliki kurtosis sama dengan 3,0. Distribusi dengan kurtosis lebih besar dari 3,0 menunjukkan data ekor yang melebihi ekor distribusi normal (misalnya, lima atau lebih simpangan baku dari mean).
Kurtosis berlebih ini dikenal dalam statistik sebagai leptokurtik, tetapi lebih dikenal sebagai "ekor gemuk." Kemunculan ekor gemuk di pasar keuangan menggambarkan apa yang dikenal sebagai risiko ekor. Distribusi dengan kurtosis rendah kurang dari 3,0 (platykurtik) menunjukkan ekor yang umumnya kurang ekstrem ("lebih kurus") daripada ekor distribusi normal.
4. Rumus
Distribusi normal mengikuti rumus berikut. Perhatikan bahwa hanya nilai rata-rata (μ) dan simpangan baku (σ) yang diperlukan.
Distribusi normal mengikuti rumus berikut:
\[ f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right) \]
Di mana:
- \( \mu \) adalah rata-rata
- \( \sigma \) adalah simpangan baku
- \( \pi \) adalah konstanta Pi (sekitar 3.14159)
- \( \exp \) adalah fungsi eksponensial
5. Contoh Distribusi Normal
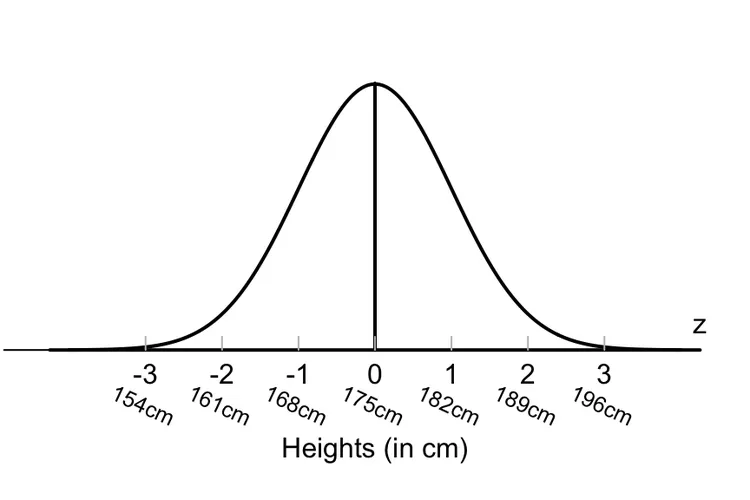
Banyak fenomena yang terjadi secara alami tampak terdistribusi secara normal. Misalnya, tinggi rata-rata manusia kira-kira 175 cm (5' 9"), menghitung baik pria maupun wanita.
Seperti yang ditunjukkan oleh grafik di bawah ini, kebanyakan orang sesuai dengan rata-rata tersebut. Orang yang lebih tinggi dan lebih pendek ada dengan frekuensi yang semakin berkurang dalam populasi. Menurut aturan empiris, 99,7% dari semua orang akan berada dalam +/- tiga simpangan baku dari mean, atau antara 154 cm (5' 0") dan 196 cm (6' 5"). Mereka yang lebih tinggi dan lebih pendek dari ini akan jarang (hanya 0,15% dari populasi).
6. Mengapa Disebut Distribusi Normal?
Distribusi normal secara teknis dikenal sebagai distribusi Gaussian, namun, istilah "normal" muncul setelah publikasi ilmiah pada abad ke-19 yang menunjukkan bahwa banyak fenomena alami tampak "menyimpang secara normal" dari mean. Ide "variabilitas normal" ini dipopulerkan sebagai "kurva normal" oleh naturalis Sir Francis Galton dalam karyanya tahun 1889, Natural Inheritance.