Uji Hipotesis Rata-rata menggunakan SPSS

Hipotesis Statistik

Hipotesis statistik merupakan suatu pernyataan tentang satu atau lebih parameter yang bisa dibuktikan secara empiris (berdasarkan data dari sampel acak). Hipotesis ini terdiri dari dua macam: Hipotesis nol (H0) dan Hipotesis alternatif (H1 atau Ha). Keputusan terhadap hipotesis ini mempunyai sifat dikotomis: Menerima (gagal menolak) H0 atau menolak H0. Bukti dari suatu pengamatan yang tidak sama dengan hipotesis yang diajukan akan membawa kita pada penolakan terhadap hipotesis tersebut. Sebaliknya, jika bukti yang diperoleh mendukung hipotesis, hipotesis tersebut diterima (gagal ditolak).

Hipotesis statistik terdiri dari dua macam bentuk, yaitu hipotesis tunggal dan hipotesis majemuk. Hipotesis tunggal menyatakan parameter dalam satu nilai tunggal pada H0 dan H1. Misalnya, H0: 800 jam dan H1: 850 jam. Sementara itu, hipotesis majemuk menyatakan suatu parameter dalam banyak nilai pada H0 dan H1. Ada tiga macam bentuk perumusan hipotesis majemuk (Wibisono, 2015).

1. Hipotesis mengandung pengertian minimum

Salah satu pabrik menyatakan bahwa rata-rata umur pemakaian lampu mereka tidak kurang dari 800 jam. Pernyataan pabrik ini ditolak jika rata-rata umur pemakaian lampu tersebut kurang dari 800 jam dan harus diterima jika lebih lama atau sama dengan 800 jam. Perumusan yang digunakan:

Hipotesis nol: \( H_0: \mu \geq 800 \text{ jam} \)

Hipotesis alternatif: \( H_1: \mu < 800 \text{ jam} \)

2. Hipotesis mengandung pengertian maksimum

Suatu perusahaan mi instan menyatakan bahwa kandungan natrium dalam produk mi instan mereka tidak lebih dari 840 gram. Pernyataan perusahaan ini akan ditolak jika rata-rata kandungan natrium pada produk mi instan mereka melebihi 840 mg dan harus diterima jika lebih kecil atau sama dengan 840 mg. Perumusan dari hipotesis ini adalah:

Hipotesis nol: \( H_0: \mu \leq 800 \text{ jam} \)

Hipotesis alternatif: \( H_1: \mu > 800 \text{ jam} \)

3. Hipotesis mengandung pengertian sama

Jika kita ingin menguji bahwa rata-rata IP mahasiswa (L) sama dengan IP mahasiswi (P), perumusan hipotesisnya adalah:

Hipotesis nol: \( H_0: \mu_l = \mu_k \)

Hipotesis alternatif: \( H_1: \mu_l \neq \mu_k \)

Hipotesis pertama disebut hipotesis satu arah-kiri, sedangkan hipotesis kedua disebut hipotesis satu arah-kanan. Sementara itu, hipotesis ketiga disebut hipotesis dua arah. Pada pengujian hipotesis, terdapat beberapa kemungkinan dari hasil menolak H0 atau gagal menolak H0.

1. Hipotesis nol (H0) benar dan penelitian yang dilakukan menunjukkan hasil bahwa kita menerima (gagal menolak) H0 sehingga kesimpulan yang diambil sudah tepat.
2. H0 benar, tetapi penelitian yang dilakukan memberikan hasil bahwa H0 ditolak sehingga keputusan ini mengandung kesalahan. Kesalahan ini disebut kesalahan jenis I. Peluang untuk melakukan kesalahan jenis I atau peluang untuk menolak H0 padahal H0 benar disebut taraf nyata/tingkat signifikan (significance level), yang dinotasikan dengan α.
3. H0 salah dan hasil penelitian menunjukkan bahwa H0 ditolak sehingga kesimpulan yang diambil sudah tepat.
4. H0 salah tetapi hasil penelitian menunjukkan bahwa gagal menolak H0 (H0 diterima) sehingga kesimpulan ini mengandung kesalahan. Kesalahan ini disebut kesalahan jenis II. Peluang untuk melakukan kesalahan jenis II dinotasikan dengan β.

Tabel Uji hipotesis satu populasi dan statistik ujinya

No	Uji hipotesis satu populasi	Statistik uji	Distribusi
1	Rata-rata dengan varians populasi diketahui	\( z = \frac{\bar{x} - \mu_0}{\sigma / \sqrt{n}} \)	normal baku
2	Rata-rata dengan varians populasi tidak diketahui	\( t = \frac{\bar{x} - \mu_0}{s / \sqrt{n}} \)	\( t_v \)
3	Varian	\( \chi^2 = \frac{(n-1)s^2}{\sigma_0^2} \)	\( \chi^2_v \)
4	Proporsi	\( z = \frac{\hat{p} - p_0}{\sqrt{p_0(1 - p_0) / n}} \)	normal baku

Secara umum, langkah-langkah dalam pengujian hipotesis adalah:

1. Rumuskan hipotesis nol dan hipotesis alternatifnya,
2. Tentukan taraf nyata (α),
3. Hitung statistik uji,
4. Tentukan daerah kritis atau daerah penolakan H0 berdasarkan taraf nyata yang ditentukan,
5. Hitung nilai statistik uji,
6. Keputusan. Ho ditolak jika nilai statistik uji termuat di dalam daerah kritis atau gagal menolak H0 jika nilai statistik uji tidak termuat di dalam daerah kritis.

Uji Hipotesis Menggunakan SPSS

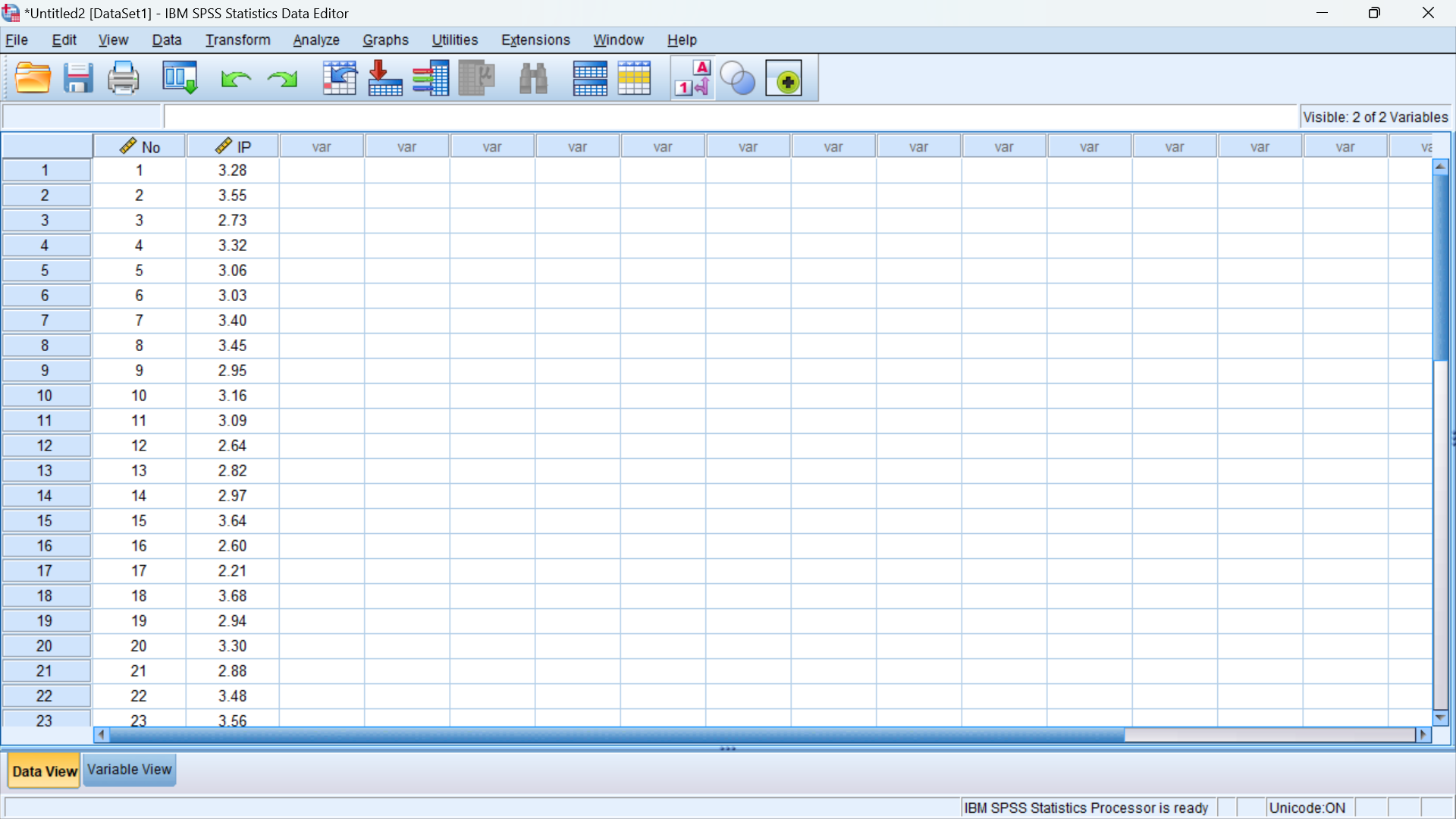
1. Input data. Dalam praktikum ini data yang digunakan adalah IP seperi gambar SPSS di bawah ini. Hipotesis yang dirumuskan adalah:

Null Hypothesis: \( H_0: 3,1 \)

Alternative Hypothesis: \( H_1: 3,1 \)

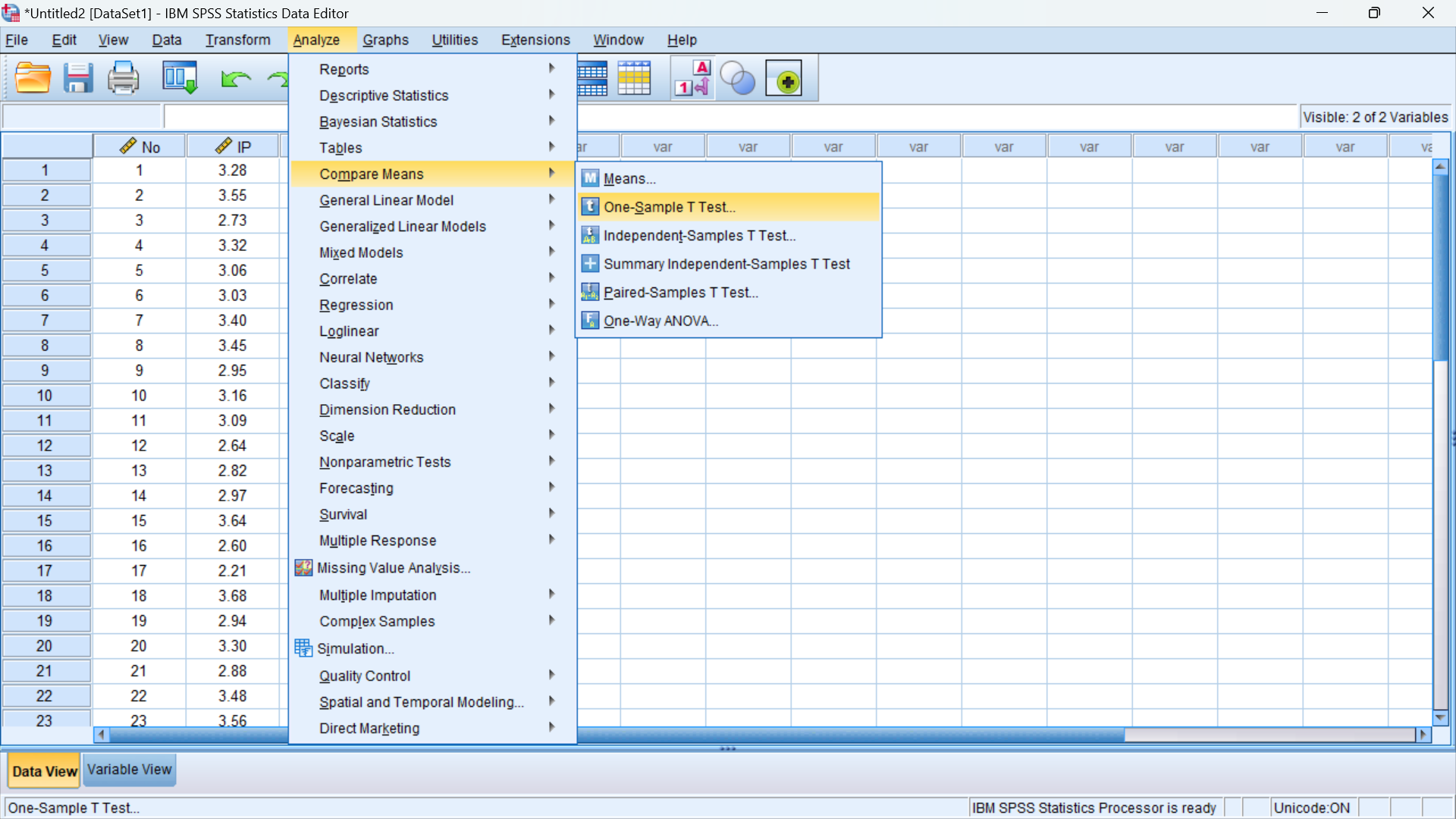
2. Menu Analyze -> Compare Means -> One Samples T Test

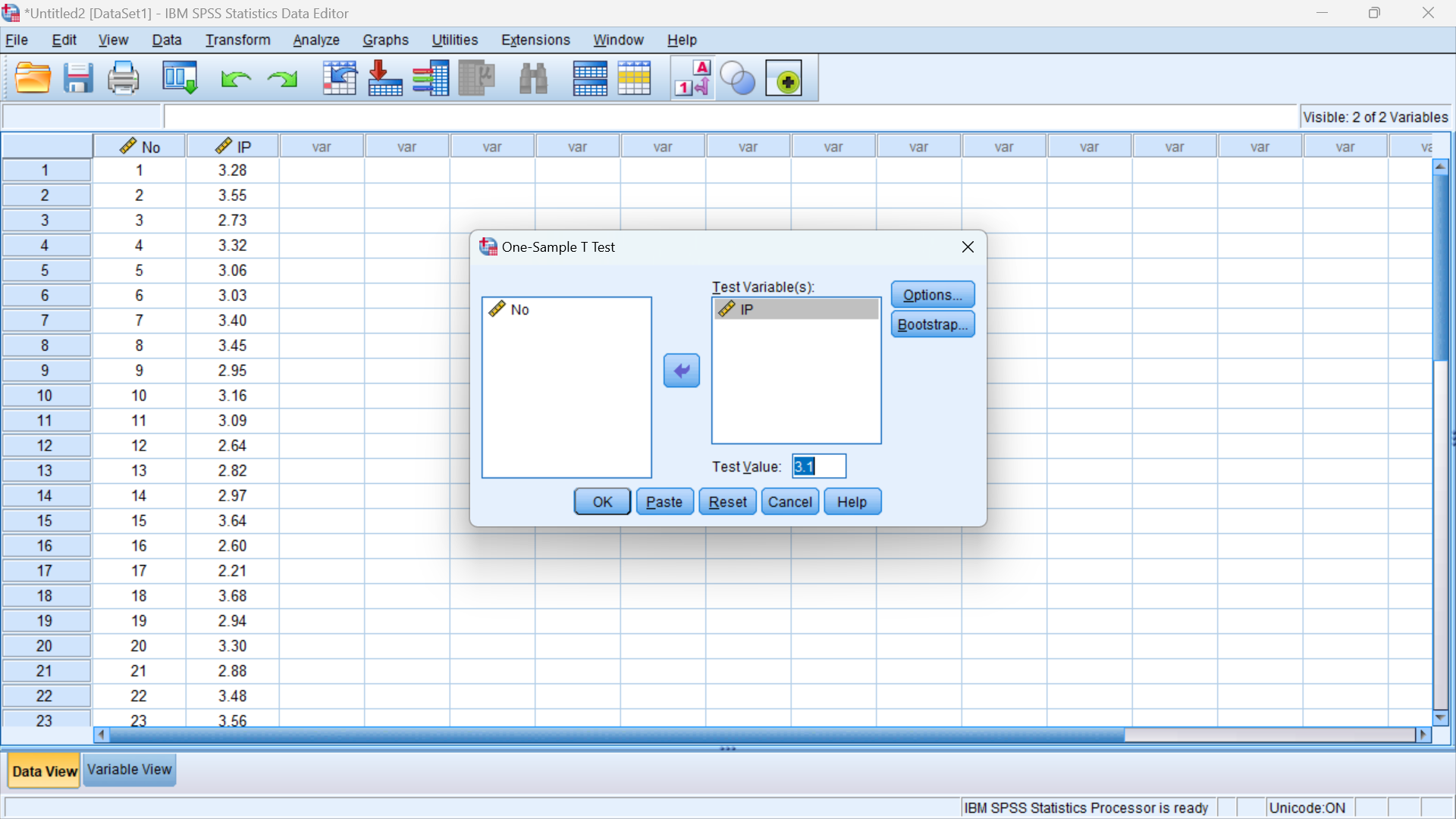
3. Pada tampilan Independent Samples T Test, Klik variabel IP -> Klik tanda panah dan Pada Test Value, isikan nilai parameter yang terdapat pada H0. Pada contoh ini, isikan angka 3,1.

5. Klik OK akan memunculkan output seperti di bawah ini.

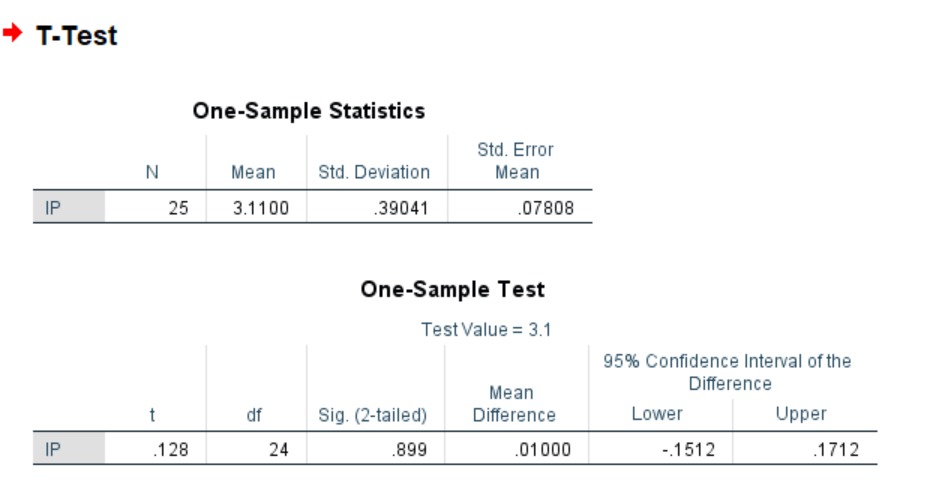
Berdasarkan pengolahan dengan SPSS, dapat diketahui bahwa nilai statistik uji t adalah 0,128 dan derajat bebasnya adalah 24. Sebelumnya telah ditentukan taraf nyata sebesar 5%. Karena pengujian hipotesisnya dua arah, nilai kritis diperoleh berdasarkan tabel distribusi t pada Tabel A.2 (Daftar Tabel Statistik) adalah \( t_{24;0.025} = 2,064\). Nilai statistik uji lebih kecil dari nilai \( t_{24;0.025} \) sehingga nilai statistik uji berada di luar daerah kritis atau di luar daerah penolakan H0. Oleh karena itu, keputusannya adalah gagal menolak H0. Ini berarti bahwa rata-rata IP mahasiswa adalah 3,1.