Membuat Boxplot Menggunakan R-Studio
Pengertian Boxplot
Boxplot atau diagram kotak merupakan salah satu jenis visualisasi data yang digunakan untuk menganalisis distribusi data serta menampilkan statistik deskriptif seperti nilai tengah, kuartil, rentang data, dan keberadaan outliers (data yang ekstrem). Diciptakan pertama kali oleh John Tukey pada tahun 1969, boxplot merupakan alat yang efektif untuk memahami sebaran data secara visual.
Fungsi Bar-Chart
-
Menunjukkan Sebaran Data: Boxplot membantu dalam menunjukkan bagaimana data tersebar secara grafis. Ini memberi gambaran visual tentang sebaran nilai-nilai data dari minimum hingga maksimum.
Identifikasi Posisi Nilai Tengah: Dengan menampilkan garis di dalam kotak, boxplot memvisualisasikan nilai median (nilai tengah) dari data, yang merupakan pemisah antara kuartil pertama dan kedua.
-
Pengukuran Kuartil dan Rentang Interkuartil: Diagram kotak memperlihatkan kuartil pertama (Q1) dan ketiga (Q3), yang membentuk kotak. Rentang interkuartil (IQR) dapat dihitung dari Q3 - Q1, menyoroti sebaran data di tengah.
Mendeteksi Outliers: Tanda-tanda titik di luar batas atas dan bawah (whiskers) menunjukkan adanya outliers atau data yang jauh dari nilai-nilai lainnya.
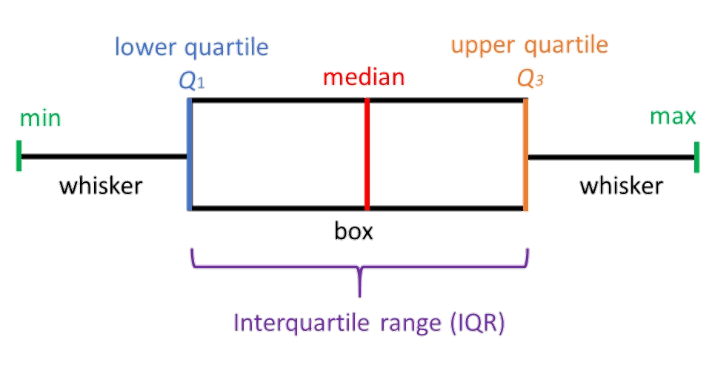
Cara Membaca Boxplot
Median: Garis di dalam kotak menunjukkan nilai tengah dari data.
Kuartil (Q1 dan Q3): Kotak mewakili 50% tengah dari data, dengan kuartil pertama (Q1) sebagai batas bawah kotak dan kuartil ketiga (Q3) sebagai batas atas.
Whiskers: Menyediakan informasi tentang sebaran data di luar kuartil. Mereka dapat menunjukkan rentang data atau batas untuk data non-outliers.
Outliers: Titik-titik yang berada di luar whiskers, menandakan data yang signifikan secara ekstrem dari distribusi.
Simetri: Jika median (garis di dalam kotak) berada di tengah kotak, dan jarak antara Q1 dan median serta Q3 dan median sekitar sama, grafik menunjukkan simetri.
-
Cenderung Miring ke Kanan (Skewness ke Kanan): Jika median lebih dekat ke Q1 daripada ke Q3 (median lebih dekat ke "atas" kotak), dan rentang data di sebelah kanan (di atas kotak) lebih panjang daripada di kiri (di bawah kotak), grafik cenderung miring ke kanan.
-
Cenderung Miring ke Kiri (Skewness ke Kiri): Jika median lebih dekat ke Q3 daripada ke Q1 (median lebih dekat ke "bawah" kotak), dan rentang data di sebelah kiri (di bawah kotak) lebih panjang daripada di kanan (di atas kotak), grafik cenderung miring ke kiri.
Boxplot dibuat di R menggunakan Fungsi boxplot()
boxplot(x,data,notch,varwidth,names,main)
Parameters
x: Parameter ini diatur sebagai vektor atau formula.
data: Parameter ini mengatur kerangka data.
notch: Parameter ini adalah label untuk sumbu horizontal.
varwidth: Parameter ini adalah nilai logis. Diatur sebagai benar untuk menggambar lebar kotak yang proposional terhadap ukuran sampel.
main: Parameter ini adalah judul dari grafik.
names: Parameter ini adalah label kelompok yang akan ditampilkan di bawah setiap boxplot.
Membuat Dataset
Pada tutorial kali ini kita menggunakan dataset yang disediakan oleh R yaitu "mtcars" dataset.
data(mtcars)
head(mtcars)
Membuat Boxplot
Sekarang kita akan membuat boxplot "mpg"
# Membuat boxplot untuk variabel 'mpg' dari dataset mtcars
boxplot(mtcars$mpg,
main = "Boxplot of MPG in mtcars",
xlab = "Mileage per Gallon")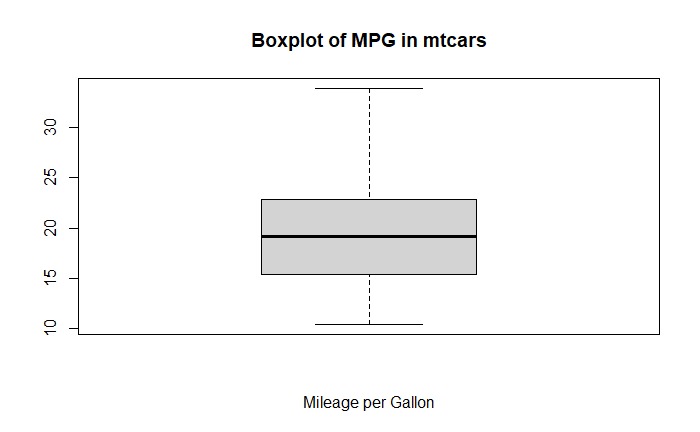
Interpretasi
Dari grafik boxplot di atas, terlihat bahwa garis tengah dalam kotak (box) mewakili nilai median dari distribusi data. Perlu diperhatikan bahwa jarak antara kuartil pertama (Q1) dan median, serta jarak antara median dan kuartil ketiga (Q3), tidak terlalu jauh. Hal ini menunjukkan adanya distribusi data yang cenderung simetris.
Dalam konteks ini, "simetris" mengacu pada distribusi data di mana nilai median (garis tengah kotak) berada di tengah-tengah atau hampir di tengah antara kuartil pertama dan kuartil ketiga. Ketika jarak antara Q1, median, dan Q3 relatif serupa, dapat diinterpretasikan bahwa sebagian besar data terletak di sekitar nilai-nilai ini, dan tidak ada kecenderungan yang kuat untuk distribusi data yang sangat condong ke satu sisi (misalnya, distribusi yang sangat miring ke kanan atau kiri).
Membuat Boxplot antara Variabel "disp" dan "gear"
Sekarang kita akan menggambarkan graph relasi antara "disp" dan "gear"
boxplot(disp ~ gear, data = mtcars,
main = "Displacement by Gear",
xlab = "Gear",
ylab = "Displacement")
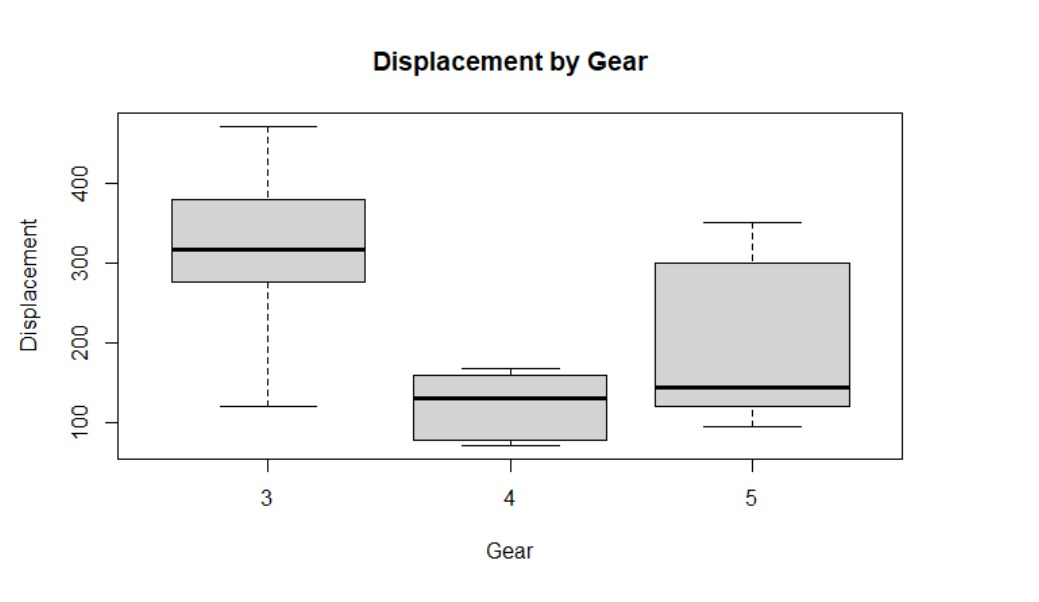
Interpretasi
Pada boxplot di atas, kita memeriksa distribusi variabel disp (displacement) berdasarkan nilai variabel gear. Dalam kategori gear 3, distribusi data cenderung simetris. Di sisi lain, untuk kategori gear 4, data cenderung condong ke kiri (skewed left), menunjukkan kecenderungan adanya nilai-nilai yang lebih rendah. Sedangkan untuk kategori gear 5, distribusi data cenderung condong ke kanan (skewed right), menunjukkan kecenderungan adanya nilai-nilai yang lebih tinggi.
Membuat Boxplot Horizontal antara Variabel "disp" dan "gear"
Sekarang kita akan menggambarkan graph relasi antara "disp" dan "gear"
boxplot(disp ~ gear, data = mtcars,
main = "Displacement by Gear",
ylab = "Gear",
xlab = "Displacement",
horizontal = TRUE)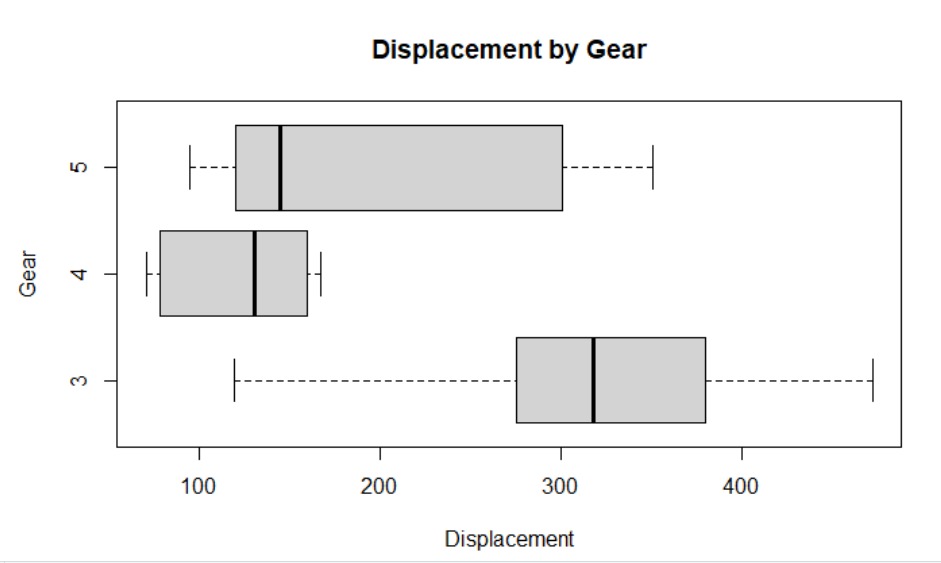
Interpretasi
Pada boxplot di atas, kita memeriksa distribusi variabel disp (displacement) berdasarkan nilai variabel gear. Dalam kategori gear 3, distribusi data cenderung simetris. Di sisi lain, untuk kategori gear 4, data cenderung condong ke kiri (skewed left), menunjukkan kecenderungan adanya nilai-nilai yang lebih rendah. Sedangkan untuk kategori gear 5, distribusi data cenderung condong ke kanan (skewed right), menunjukkan kecenderungan adanya nilai-nilai yang lebih tinggi.